Theta is one of the most critical concepts in option and structured product pricing, representing the rate at which an option's value changes over time. The concept of Theta is rather different from the other Greeks we have already examined in that it does not represent a sensitivity that needs to be hedged. Instead, it is an important property of the pricing of structured products and options which needs to be evaluated and taken into account.

Theta measures the expected daily decrease in an option's price after a small length of time (or equivalently the reduction in remaining maturity), assuming all other factors remain constant. It is typically a negative number for long vanilla call and put option positions, reflecting the diminishing value of options as they approach expiration.

For structured products, Theta is usually negative for capital-protected products and positive for capital-at-risk products. This is because such products have net positive and negative option positions, respectively, resulting in a situation similar to the vanilla option case.

Understanding time decay in options

Negative Theta, often referred to as “time decay”, occurs because options can be considered time-wasting assets, certainly if bought at or out of the money. Their value consists of two components: intrinsic value (the difference between the strike price and the underlying asset's price for a call option) and extrinsic or time value. Time value captures the convexity of an option price in that a large price movement in the right direction will benefit the product. As expiration approaches, the extrinsic value gradually diminishes until only intrinsic value remains.

We can illustrate this for a call option with a strike of 100 with two years remaining until maturity.

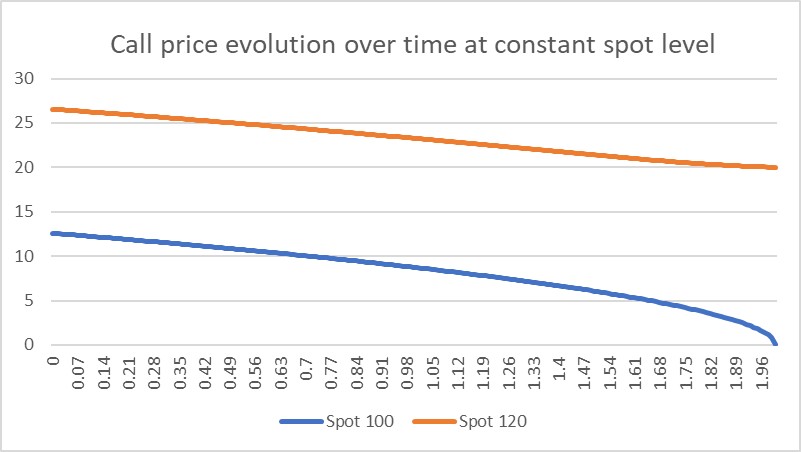
The two curves represent the price change, assuming a constant spot level at 100 and 120, respectively, as two years pass and the option approaches maturity.

The option price is higher when the spot price is at 120 compared to when it is 100, as is to be expected. However we can see that the shape of the curves are rather different, with the price at the spot of 100 falling off quickly towards maturity.

These observations about the option price movement are confirmed by examining the Theta curve, which represents the rate of change of the first chart. The curve for the spot value of 120 shows little change over time, therefore its Theta remains relatively small. However, for the at-the-money case, we see a significant increase in Theta at maturity.

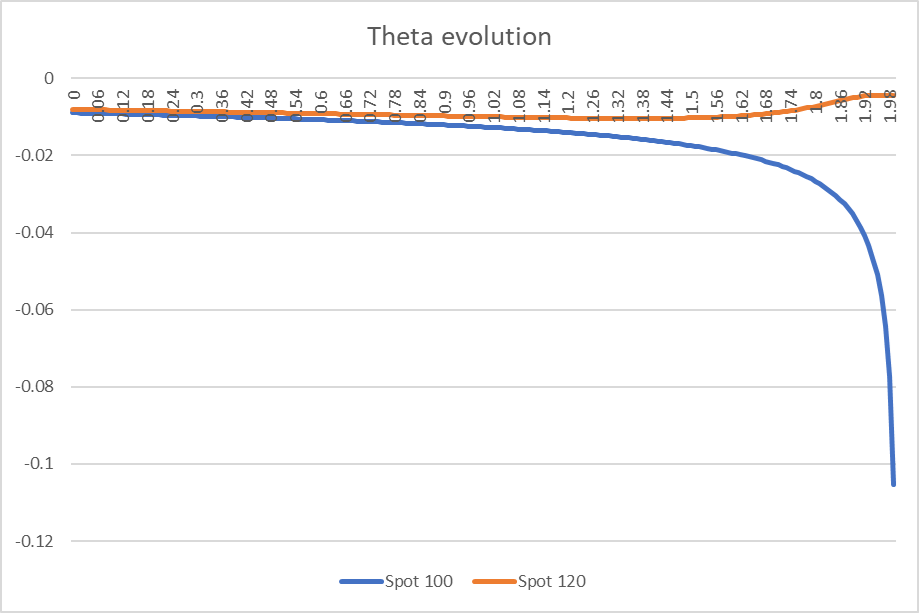
Theta decay is not generally linear but accelerates for the at-the-money case as expiration approaches. Theta decay is most pronounced for at-the-money options or structured products and is less important for in-the-money options, which retain their intrinsic value and out-of-the-money options that have little value to lose in the first place.

Theta is also higher when volatility is greater, as there is more time value to lose. If an underlying remains relatively static over time, it behaving like it has near-zero volatility is more costly.

Autocallables and Theta spikes

The picture for Theta is made more complicated for structured products due to the combination of option positions and potential path dependency. The observation that Theta is generally positive for capital-at-risk products holds because if the underlying stays constant then no further barriers will be breached. For a structured product where the underlying is close to but above the barrier, Theta tends to be higher because of the proximity of the barrier means that if it is avoided the product will gain in value significantly. The behaviour of Theta for auto-calls is more complex still. The Theta profile for an auto-call changes dramatically based on the underlying asset's price path and proximity to auto-call levels. This creates time "zones" of theta sensitivity that change throughout the product's life.

When a product approaches an auto-call observation date, Theta effects can become significantly magnified. If the underlying asset trades just below the call barrier as an observation date approaches, Theta can become extremely negative. The exact magnitude of this effect depends on the payment amount and the remaining auto-call levels and payments.

Theta will be concentrated in the days immediately preceding observations dates, creating Theta "spikes". If the product does not auto-call, Theta will begins building toward the next observation date, resulting in a series of cycles throughout the product's life.

Because Theta does not have a direct hedging implication that comes out of Theta (unlike Delta and Gamma for underlying moves and Vega for volatility, for example), this is not a Greek that demands constant attention from traders.

However, Theta does show the evolution of structured product prices assuming all other parameters remain constant, offering an interesting picture of the current position and how value may be slowly gained or lost.